LO-phonon induced resonant scattering of electrons between Landau levels, also called the magnetophonon (MP) effect, has been widely used to obtain information on band structure parameters such as the effective mass and the electron-LO-phonon interaction in bulk and two-dimensional semiconductors. The magnetophonon effect has proved to be a useful magnetotransport tool for the determination of effective masses and is moreover particularly suitable to carry out investigations of the temperature dependence of m* in a temperature range which is commonly not accessible to other methods such as cyclotron resonance measurements.

In 2D systems such as quantum wells and single heterojunctions the magnetophonon effect has been used not only to measure effective masses of 2D electrons [1], but also to investigate the influence of various scattering mechanisms on the high temperature transport properties of these systems. Evidence has been found that interface phonons are especially effective in the MP resonant scattering in heterostructures and their frequency has been determined [2]. The self consistent consideration of all scattering mechanisms in the calculation of the high temperature magnetoresistance leads to the prediction of the collapse of MP oscillations at high magnetic fields, and excellent agreement between theory and experiment has been obtained [3], [4].

In quasi-one-dimensional electron gases (1DEGs) the investigation of magnetophonon resonances (MPR) is considered as an useful magnetotransport tool for the determination of the energy difference between adjacent 1D subbands arising from the lateral confinement. It can be shown that the lateral quantization leads to a shift of the magnetic field positions of the resonant extrema in the high temperature magnetoresistance. Under certain premises this shift is proportional to the subband spacing E₀ and provides a particularly simple method to determine E₀. This is particularly useful in those cases where, due to a very low electron density or relatively high subband spacing, only a small number (less than, say, four) of subbands is occupied in the quantum wire. In these cases the standard magnetic depopulation (MD) method, commonly used to estimate the subband spacing, is no longer a suitable transport technique for the characterization of quantum wires. The MD method exploits the oscillatory structure in the low temperature magnetoresistance occurring when the magnetoelectric hybrid levels are successively shifted across the Fermi level by increasing the magnetic field. A small number of occupied subbands drastically reduces the oscillatory structure in R_xx(B) and thus, the commonly used evaluation methods [5], [6] cannot be applied any more.

The samples used in this work were conventional modulation doped heterostructures on which arrays of 40 quantum channels were fabricated by laser holography and wet chemical etching. The electron mobility and electron density of the unstructured samples are 1.6 x 10⁶ cm²/Vs and 1.1 x 10¹¹ cm^-2, respectively, at 4.2 K. The measurements of the magnetoresistance were performed using a standard constant current procedure and a cryostat equipped with a variable temperature inset and a superconducting magnet which allowed magnetic field strengths up to 10 T. For measurements at variable electron densities, an array of wires has been fabricated which were completely depleted at 4.2 K due to the low carrier concentration of the underlying heterostructure. This allows to obtain the same set of wires at different electron densities if carriers are generated by illumination using a light emitting diode. After illumination, the samples were slowly heated to temperatures between 100 K and 160 K. When equilibrium, i.e. stable sample resistance, was reached the magnetoresistance was measured showing a distinct structure due to the magnetophonon effect. Subsequent to the high temperature measurement, the samples were cooled down slowly to T = 2 K and a magnetic depopulation (MD) measurement was performed to determine the electron density. Then the temperature cycle was repeated, while further gradual reduction of the carrier density was achieved by maintaining the sample at 180 K for several hours before the next MPR experiment at T near 100 K was performed.

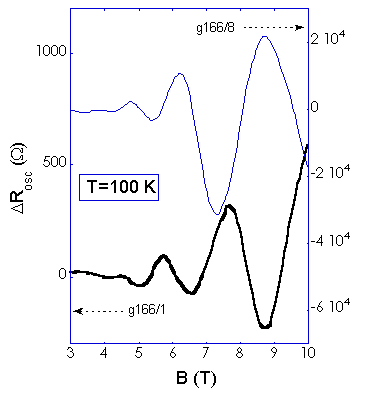
Typical data are shown in Fig. 1. As first striking feature, we find a strong dependence of the strength of the observed magnetophonon oscillations on the used sample structure and the preparation process. The effect is most pronounced in samples where the remote impurity scattering is reduced as far as possible by e.g. low doping and large spacer layers. We explain this observation by the fact that all kinds of additional scattering lead to a broadening of the density of states of magnetoelectric hybrid levels in the wires which smears out the MPR oscillations. Since the wet chemical etching, by which the confinement of the wires is achieved, induces additional sources of scattering such as a considerable surface roughness, it is clear that deeper etching on the purpose to get a stronger confinement will weaken or eventually destroy the magnetophonon effect in the wires. This is exactly what we observed. In Fig. 1, the oscillatory part of R_xx, normalized to the zero field resistance R₀, is shown for two samples which differ only by the depth of the etch pits. When only slightly deeper etching is done, the amplitude of the resonances is reduced by almost an order of magnitude. Thus, to observe sufficiently pronounced MPRs we had to restrict ourselves to the case of relatively weak confinement, i.e. wires displaying subband energies in the range of 1 meV.

Fig. 1: Oscillatory part R_osc of the magnetoresistance at T = 100 K for two different samples, obtained after subtraction of the background resistance and normalization to the zero field resistance R₀. The two samples differ by the depth of the etch pits defining the lateral confinement. For g166/1 approximately 85 Å of the cap layer were removed, for g166/8 the etching depth is only 70 Å. Note the different scaling of the y-axes.

The main purpose of this work was to verify that the magnetophonon effect can be used to determine subband energies of quantum wires with small numbers of subbands occupied. We therefore compare the results of a high temperature measurement with those of a magnetic depopulation measurement performed at 2 K. Fig. 2 (a) shows a plot of the squared magnetic field positions of the resonant minima in the oscillatory part of R_xx measured at T = 100 K versus the inverse squared index N which is defined according to the generalized resonance condition (see e.g.[1]) , with E_LO = 36.6 meV being the LO phonon energy in bulk GaAs, and E₀ the subband spacing of the 1D wires. As seen from Fig. 2 (a), the measured resonance positions lie clearly on a straight line and may therefore be analyzed in terms of the above resonance condition which can be rewritten in the following form :

.

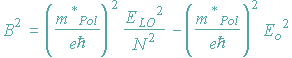According to this formula, the slope of the straight line is a measure of the polaron mass in the quantum wire, whereas its intersection with the B²-axis gives the subband spacing E₀. It should be emphasized that this simple relationship is only valid if the confining potential can be approximated by a parabolic well. Another major approximation made is the assumption that the energy of the LO phonons is not influenced by the additional confining potential and can be taken to be the same as in bulk GaAs. With these assumptions we obtain from the data shown in Fig. 2 (a) a polaron mass of 0.069 m_e and a subband spacing of 1.6 ± 0.3 meV which is enhanced in comparison to the corresponding value obtained from a subsequent magnetic depopulation experiment (1.1 ± 0.3 meV). This enhancement was found in all investigated samples where a direct comparison was feasible and the subband spacings determined from MPR lie some 30% above those extracted from magnetic depopulation experiments.

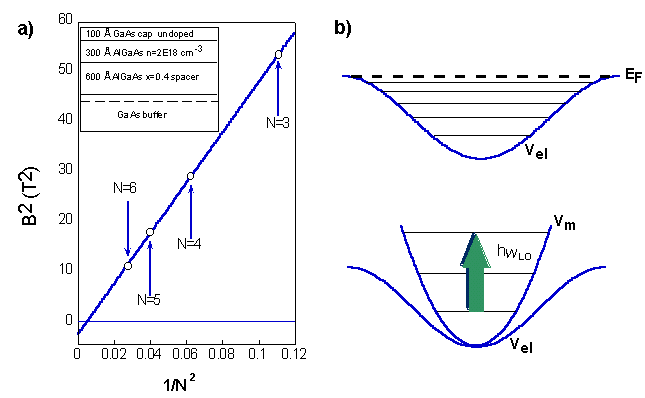
Fig. 2: (a) Plot of the squared magnetic field positions of the minima in R_osc versus the inverse squared index N explained in the text. The inset shows the sample structure. (b) Schematic potential forms used in the text to explain the difference in the subband spacing obtained by magnetophonon resonance and magnetic depopulation measurements.

Since temperature effects on the confining potential are small unless considerable recharging and reordering of electrically active impurities occurs [7], this difference can be explained by the following considerations (Fig. 2 (b)): The confinement in the investigated samples is obtained by very shallow etching leading to a relatively weak confining potential. From self consistent calculations reported earlier [8] it is known that the potential shape should be sinusoidal instead of simply parabolic. This in turn implies that the subbands near the upper edge of the confinement potential are closer to each other than they are at the bottom where the potential is parabolic to a good approximation. In MD experiments the subband spacing is estimated from the deviation of the low field minima in R_xx from the behavior observed in unstructured 2DEGs. In this case the value obtained for the subband spacing is determined by the depopulation of subbands lying near the upper edge of the confining potential which occurs at fairly low magnetic fields. MPR, on the other hand, are observed at the other end of the magnetic field scale where the magnetic confinement dominates the electrostatic one. Also electrons at the bottom of the confining potential can undergo resonant LO phonon scattering processes into empty states 36 meV higher in energy. Due to the increased density of states in high magnetic fields, a reduced number of subbands is occupied. They correspond to those states located deep in the confining potential where it is well described by a parabolic form. At high magnetic fields the deviation of V_el from the parabolic form is therefore negligible and the subband spacings determined from MPR correspond to those near the (parabolic) bottom of the confining potential which are larger than those estimated from MD experiments.

Fig. 3: Dependence of the subband spacing on the one dimensional carrier density in the wires determined by MPR experiments (open circles) and magnetic depopulation experiments (solid circles). The latter could be obtained only if sufficient numbers of subbands were occupied in the wires to apply standard evaluation methods. The straight line is the result of a linear fit to the values and is only a guide to the eye. The arrow indicates the regime, were MD measurements were not possible.

Using the procedure described in the experimental part of this paper the dependence of the subband spacing on the electron density in the quantum wires was investigated. The results of these measurements for sample g166/8 are displayed in Fig. 3. The E₀ values plotted in this figure are taken from MPR measurements at T = 100 K (open circles) as well as MD experiments at T = 2K (solid circles). From the latter we could get this information only if a sufficient number of subbands was occupied to apply the evaluation method proposed by Berggren et al. [8]. The solid line drawn in Fig. 3 stems from a linear fit to the data and is only intended as a guideline to the eye.

The observed increase of the subband spacing with decreasing electron density has been predicted by self consistent calculations [9] and can be qualitatively explained as follows: The confining potential is formed by a periodic modulation of the donor distribution induced by the etching process. If the presence of conduction electrons in the so defined 1D channels is taken into account self consistently, the bare potential of this positive space charge is partially screened out. Therefore, the confinement will be the stronger the less electrons are present in the wire. Note that the same behavior of E₀ as a function of n_1D is also observed for various samples with different wafer structure, when the electron density is varied by alternative methods, e.g. by applying a back gate voltage.

In summary, we have used the magnetophonon effect to investigate the energy spectrum of quasi-one-dimensional electron systems. A systematic study of the dependence of the 1D sublevel spacing on the channel electron density was performed. By variation of the electron density in the wires through illumination with a red LED the 1D subband spacing, as determined from magnetophonon resonance measurements, is found to increase with decreasing electron density. Further, the subband spacing determined by MPR is found to be systematically higher than the subband spacing obtained from simultaneous magnetic depopulation measurements. It was further demonstrated that the combination of the two transport methods provides a particularly simple way to obtain direct information on the shape of the underlying electrostatic confinement potential in a way that MD measurements probe the subband spacing at the Fermi level and MPR measurements the subband spacing at the bottom of the confining potential.

The authors are indebted to Frank Stern for performing self-consistent calculations of confinement potentials and electron density distributions and for helpful discussions on the subject. Thanks are also due to J. C. Portal, Y. Levinson, J. Allen, P. Streda and W. Boxleitner for numerous discussions.

[1] D.C. Tsui, Th. Englert, A.Y. Cho, A.C. Gossard, Phys. Rev. Lett. 44, 341 (1980)

[2] M.A. Brummell, R.J. Nicholas, M.A. Hopkins, J.J. Harris, C.T. Foxon, Phys. Rev. Lett 58, 77 (1988)

[3] W. Xu, F.M. Peeters, J.T. Devreese, D.R. Leadley, R.J. Nicholas, Int. J. Mod. Phys. B 10, 169 (1996)

[4] D.R. Leadley, R.J. Nicholas, J. Singleton, W. Xu, F.M. Peeters, J.T. Devreese, J.A.A.J. Perenboom, L. van Bockstal, F. Herlach, J.J. Harris, C.T. Foxon, Phys. Rev. Lett. 73, 589 (1994)

[5] K.F. Berggren, D.J. Newson, Semicond. Sci. Technol. 1, 327 (1986)

[6] K.F. Berggren, G. Roos, H.van Houten, Phys. Rev. B 37, 10118 (1988)

[7] G. Berthold, J. Smoliner, C. Wirner, E. Gornik, G. Böhm, G. Weimann, M. Hauser,

[8] J. Smoliner, G. Berthold, F. Hirler and N. Reinacher, Semicond. Sci. Technol. 6, 642 (1991)

[9] J. Smoliner, G. Berthold, F. Hirler and N. Reinacher, Semicond. Sci. Technol. 6, 642 (1991)

Institut für Festkörperelektronik, Technische Universität Wien

1. G. Ploner, J. Smoliner, G. Strasser and E .Gornik: "Transport Characterization of Quantum Wires by Magnetophonon and Magnetic Depopulation Experiments", Proc. ICSMM9, Liege (1996) Superlatt. Microstruct. 22, 2 (1997)
2. G. Ploner, J. Smoliner, G.Strasser, M. Hauser and E. Gornik: "Energy levels in quantum wires studied by magnetophonon effect" to appear in Phys. Rev. B. (1998)
3. C. Eder, J. Smoliner, R. Heer, G. Strasser, E. Gornik: "Probing of Superlattice Minibands by Ballistic Electron Emission Microscopy", Proc. MSS8, Santa Barbara (1997), to be published in Physica E (1998)
4. R. Heer, C. Eder, J. Smoliner, E. Gornik: "A floating electrometer for scanning tunneling microscope applications in the femtoampere range", Rev. Sci. Instruments 68, 4488 (1997)
5. J. Smoliner, C. Eder, G. Strasser, E.Gornik: "BEEM on quantum wires", Proc. HCIS10, Berlin (1997) Phys. Stat. Sol. 204, 386 (1997)

1. C. Eder, J. Smoliner, R. Heer, G. Strasser, E. Gornik: "Probing of Superlattice Minibands by Ballistic Electron Emission Microscopy", MSS8, Santa Barbara (1997)
2. J. Smoliner, C. Eder: "Ballistic electron emission microscopy using InAs tips.", Int. Conf. STM97, Hamburg (1997)
3. J. Smoliner, M. Hauser, C. Eder, G. Strasser, E. Gornik: "Quantum dot structures for STM tips", PHASDOMS 97, Aachen, Germany, 1997
4. C. Eder, J. Smoliner, R. Heer, G. Strasser, E. Gornik: "Probing of Superlattice Minibands by Ballistic Electron Emission Microscopy", Int. Conf. STM97, Hamburg (1997) (Poster)
5. R. Heer, C. Eder, J. Smoliner, E. Gornik: "A high precision electrometer for scanning tunneling microscope applications in the femtoampere range", Int. Conf. STM97, Hamburg (1997) (Poster)
6. J. Smoliner, C. Eder, G. Strasser, E. Gornik: "BEEM on quantum wires", HCIS10, Berlin (1997)
7. G. Ploner, J. Smoliner, G. Strasser, M. Hauser, E. Gornik: "Charakterisierung von Quantendrähten mittels Magnetophonon Effekt", Österreichische Physikalische Gesellschaft, 47. Jahrestagung, Wien, Austria (9/97)

1. C. Eder, Raster-Tunnelspektroskopie an niedrigdimensionalen Elektronensystemen (Nov. 1997)

1. J. Smoliner, Current transport in nanostructures, TU-Wien, Fakultät für Elektrotechnik, 16.04. 97